triadabot.blogg.se

Let us take a closer look at our assumed plane wavefront.

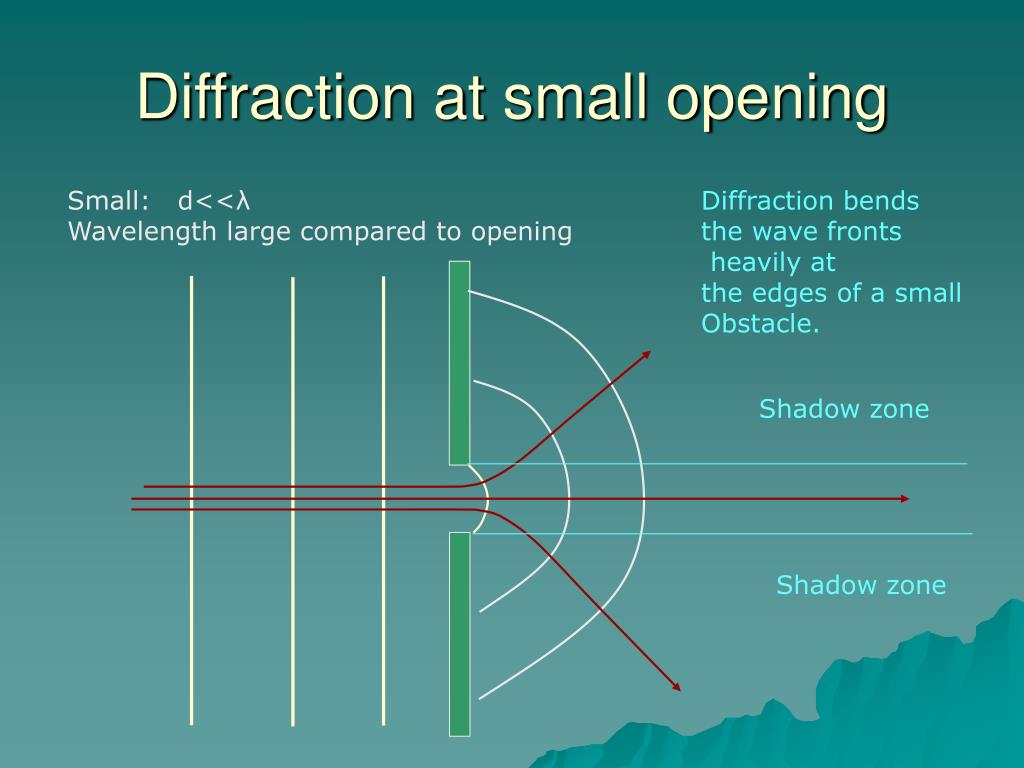
Obstacles with a size similar to the wavelength show a much more complicated impact on wave propagation. Obstacles that are very small compared to the wavelength have no influence on wave propagation. The angle of incidence is equal to the exit angle. A ray-tracing model covers this perfectly. Such large obstacles compared to the wavelength indeed act like mirrors to the sound. Think of an ocean wave that hits a rocky beach. At normal incidence, the SPL directly at the wall is twice that of the incoming wavefront. Ray tracingĪ wall that is much larger than the wavelength reflects the wave backwards. To simplify our discussions as before (Link wavelength), we assume the signal carried by the wave to contain only a single frequency. Our consideration starts with a plane wavefront that hits a stiff, heavy and flat wall at normal incidence. Therefore, objects in our daily environment influence sound propagation differently: they both reflect and diffract sound, depending on shape and size relative to the sound signal’s wavelength. The easiest way to describe sound propagation is by comparison with light rays.īut the wavelength of light is far below a millimeter while that of sound ranges from millimeters to meters. Interestingly, sound waves bend around objects. So, it makes sense that lower-frequency sounds typically have a wide dispersion and sounds with small wavelenths have a narrow dispersion.A complex mixture of reflection and diffraction happens to sound that hits an object of similar dimension as the wavelengths of the sound signal. Conversely, if the ratio of W/D is small, then x is small and the waves are said to have a narrow dispersion and the sound waves go through the opening without spreading out very much. In this case, the waves are said to have a wide dispersion and the sound waves are spread out wider through the opening. If the ratio of W/D is large, then x is large. So, looking at these two equations you can tell that the extent of the diffraction depends on the ratio of the wavelength to the size and shape of the opening. Angle x, W for wavelength, and D for width are all still the same. For a circular opening, the equation is slightly different. Gives x in terms of the wavelength and the width of the doorway. If we let angle x be the location of the first minimum intensity point on either side of the center, W be the wavelength, and D be the width of the doorway, the equation Waves diffract differently depending on the object they are bending around. Each maxima gets progressively softer further away from the center. As you move further away from the center, the intensity decreases until it is at zero, then increases to a maximum, falls to zero, rises to a maximum.and so on. Directly in front of the center of the doorway the intensity is a maximum. The sound outside of the room has varying intensity depending on where you stand.

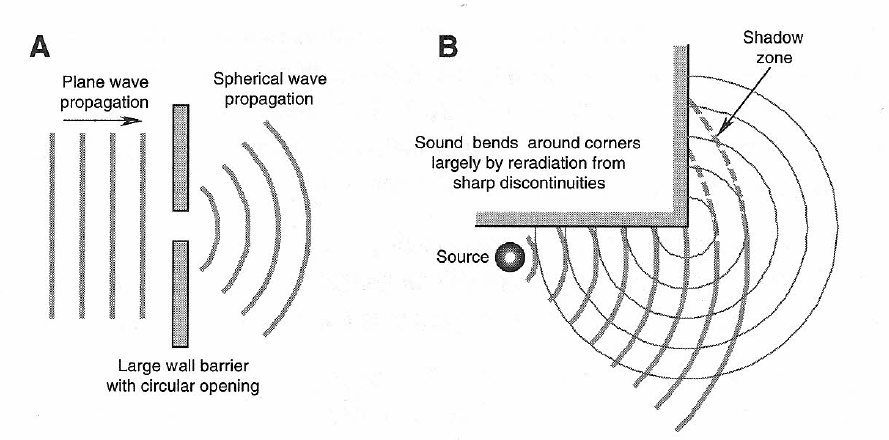
The final result is the diffraction of the sound wave around the doorway. This results in each molecule producing a sound wave and emitting it outward in a spherical fashion. This means that each air molecule is a source of a sound wave itself. Instead, the air in the doorway is set into longitudinal vibration by the sound waves from the stereo. Without diffraction, the sound from the stereo could only be heard directly in front of the door. All waves exhibit diffraction, not just sound waves. This bending of a wave is called diffraction. For example, if a stereo is playing in a room with the door open, the sound produced by the stereo will bend around the walls surrounding the opening. An obstacle is no match for a sound wave the wave simply bends around it.